Slack-Free Spiking Neural Network Formulation for Hypergraph Minimum Vertex Cover

Abstract

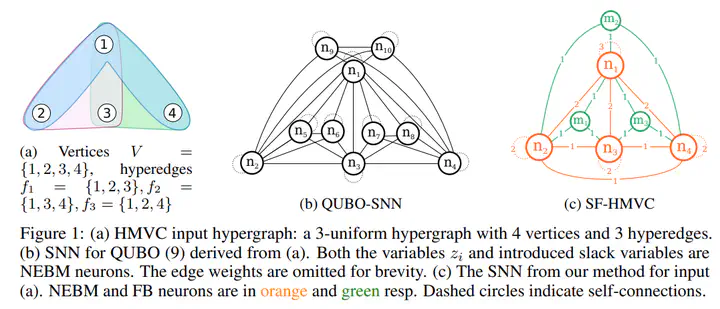
Neuromorphic computers open up the potential of energy-efficient computation using spiking neural networks (SNN), which consist of neurons that exchange spike-based information asynchronously. In particular, SNNs have shown promise in solving combinatorial optimization. Underpinning the SNN methods is the concept of energy minimization of an Ising model, which is closely related to quadratic unconstrained binary optimization (QUBO). Thus, the starting point for many SNN methods is reformulating the target problem as QUBO, then executing an SNN-based QUBO solver. For many combinatorial problems, the reformulation entails introducing penalty terms, potentially with slack variables, that implement feasibility constraints in the QUBO objective. For more complex problems such as hypergraph minimum vertex cover (HMVC), numerous slack variables are introduced which drastically increase the search domain and reduce the effectiveness of the SNN solver. In this paper, we propose a novel SNN formulation for HMVC. Rather than using penalty terms with slack variables, our SNN architecture introduces additional spiking neurons with a constraint checking and correction mechanism that encourages convergence to feasible solutions. In effect, our method obviates the need for reformulating HMVC as QUBO. Experiments on neuromorphic hardware show that our method consistently yielded high quality solutions for HMVC on real and synthetic instances where the SNN-based QUBO solver often failed, while consuming measurably less energy than global solvers on CPU.

Anh-Dzung Doan

Postdoctoral Researcher

My research interests lie in the area of robotic vision, at the intersection of robotics, computer vision, and machine learning.